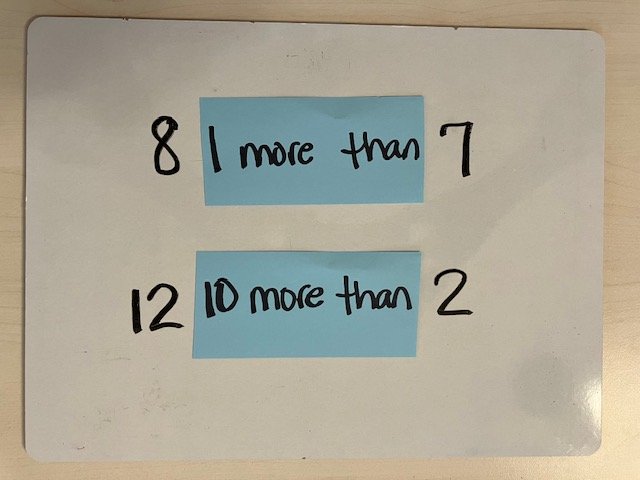Tutoring and Math: Vertical Alignment and Sequencing Numbers

This week I want to briefly discuss the vertical alignment of the math core curriculum.  

I am going to take one concept, knowing how numbers behave on a number line, and demonstrate how learning in earlier grades can influence the learning of sixth grade students. Also, I will highlight how gaps in foundational knowledge impact learning and how targeted interventions can help.

Please note that when I say how numbers behave, I am referring to the predictable pattern of ascending and descending numbers and their values on a number line. 

Let’s start with the sixth grade math core curriculum standard. This standard includes coordinate planes, but for this blog, I will only cover horizontal number lines.

6.NS.C.6:  Understand a rational number as a point on the number line.  Extend number line diagrams and coordinate axes familiar from previous grades to represent points on the line and in the plane with negative number coordinate.  

6.NS.C.6.a:  Recognize opposite signs of numbers as indicating locations on opposite sides of 0 on the number line; recognize that the opposite of the opposite of a number is the number itself.

6.NS.C.6.c:  Find and position integers and other rational numbers on a horizontal or vertical line diagram

An example of integers plotted on a horizontal number line.

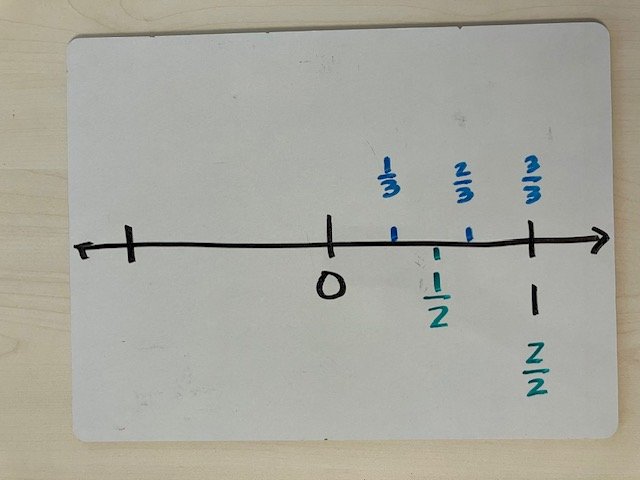
According to this standard, sixth grade students need to understand what rational numbers are and plot them on a number line.  This means that students need to know that rational numbers include natural numbers, whole numbers, fractions, decimals and integers.  Sixth grade students also need to recognize the value of a given number in order to plot the number on a number line relative to the other numbers on that line.  For example, they need to understand that ½  is halfway between 0 and 1, and ⅔ is greater than ½,  two of three units away from 0, but one unit away from 1.  They cannot plot ⅔ as halfway between ½  and 1 because that is a different number, ¾.

Students need to understand the value of a number in order to plot it accurately on a number line.

In order to accurately position rational numbers on a number line, students have to be able to compare and contrast number values to properly sequence and position them. This foundational skill is initially developed in kindergarten, K.CC.A, when students learn to count ascending numbers in sequence and represent numbers with the correct amount of objects. In first and second grade, students learn to compare, contrast, and order numbers by examining the digits in the ones, tens, and hundreds positions. In addition, students in first and second grade need to fluently increase and decrease numbers by 10s and 100s, (1.NBT.B.2, 1.NBT.B.3, 1.NBT.C.5, 2.NBT.A.1, 2.NBT.A.4, 2.NBT.B.8).

In first grade, students need to compare and order numbers by tens and ones in addition to increasing and decreasing numbers by one and ten.  

In second grade, students go into more detail comparing numbers by their place value in order to determine the relationship between the numbers sequence them.   

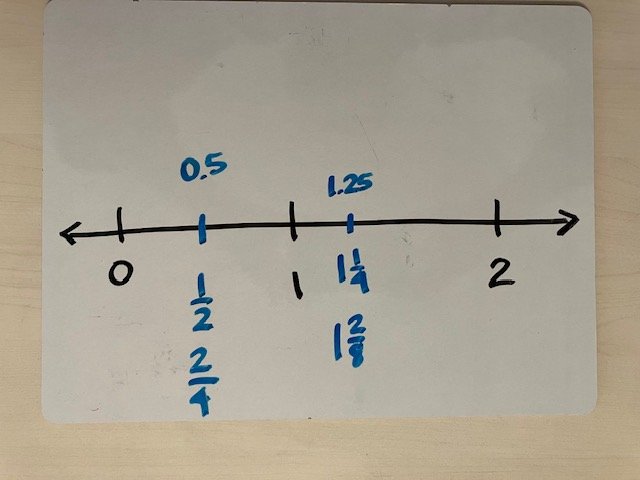
In third grade, students are required to plot fractions on a number line and compare and explain equivalent fractions (3.NF.A.2). In fourth and fifth grades, comparing, contrasting, and sequencing numbers is expanded to include other fractions, equivalent fractions, decimals and multi-digit numbers (4.NF.A, 4.NF.C, and 5.NBT.A).

Understanding how equivalent fractions and decimals may share a position on a number line is foundational skill for accurately plotting rational numbers on a number line. 

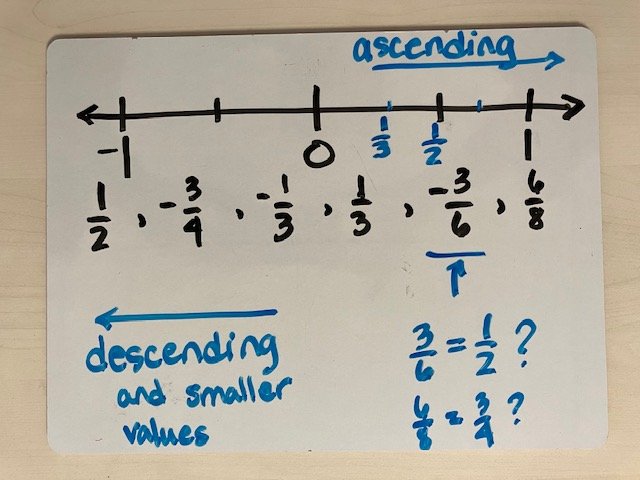
If sixth grade students are struggling with comparing and ordering numbers to plot them on a number line, I need to determine if they are confusing the positional value of a digit in a number (its place value), confusing fractions because they still assume that the larger the denominator, the larger the fraction, or are they just confused about the ascending and descending values of negative numbers? Answering these questions will help inform my next steps.

Plotting positive and negative fractions on a number line accurately.  

This is a simplified explanation of how the math common core is vertically aligned and how each piece of the core is foundational to the learning that students will have in later grades.  As a Special Educator and tutor, I look for that foundational understanding when working with students.  When students are getting confused and struggling to learn new content, I need to review their foundational knowledge to determine what is missing. Then I can develop and start interventions that will help students build that foundational knowledge so they can be successful going forward.

If your child is struggling with grade level math content, send me a message or give me a call for a free consultation on how I can help.